Table of Links
3.2 Measuring Learning with Coding and Math Benchmarks (target domain evaluation)
3.3 Forgetting Metrics (source domain evaluation)
4 Results
4.1 LoRA underperforms full finetuning in programming and math tasks
4.2 LoRA forgets less than full finetuning
4.3 The Learning-Forgetting Tradeoff
4.4 LoRA’s regularization properties
4.5 Full finetuning on code and math does not learn low-rank perturbations
4.6 Practical takeaways for optimally configuring LoRA
Appendix
D. Theoretical Memory Efficiency Gains with LoRA for Single and Multi-GPU Settings
4 Results
4.1 LoRA underperforms full finetuning in programming and math tasks
We compare LoRA and full finetuning after performing an exhaustive learning rate sweep for each method, which we found to be crucial (Dettmers et al., 2024). We include learning rate sweep results in Figure 8.
\ We perform a sample-efficiency analysis – i.e., compute the learning metrics as a function of training samples seen – for both LoRA and full finetuning. For IFT, we train separate models for 1, 2, 4, 8, 16 epochs. For CPT, we manipulate the number of unique tokens (0.25, 0.5, 1, 2, 4, 8, 16, 20 billion), using individual learning rate cooldown schedules. We train six LoRA models for each condition (3 target modules [“Attention”, “MLP”, and “All”] × 2 ranks [16, 256]).
\ 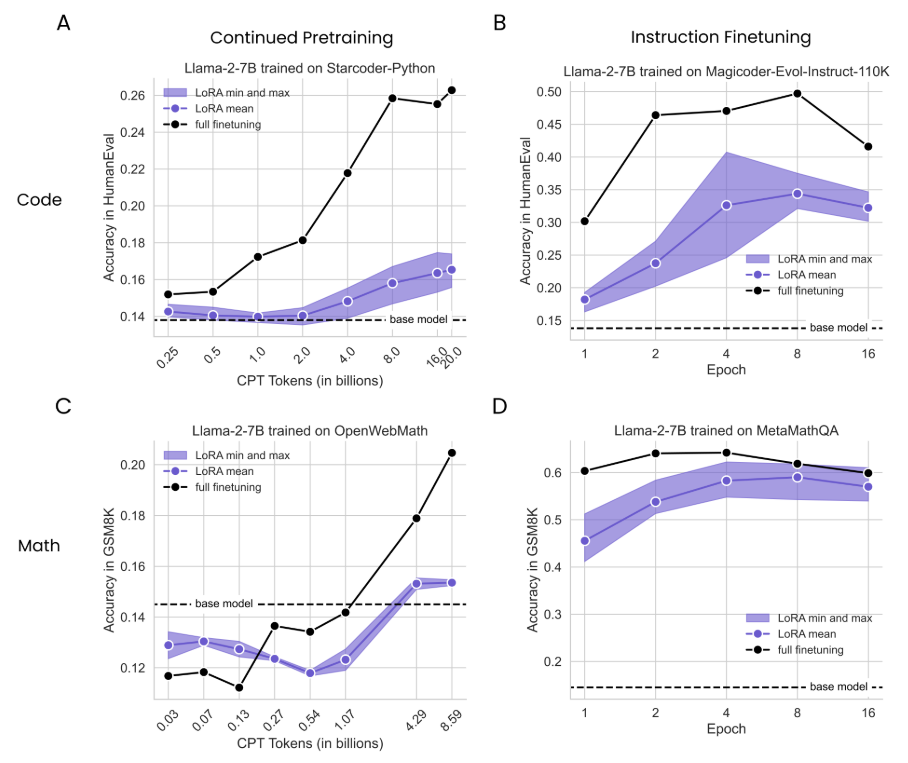
\ In Fig. 2, we summarize the performance of the six LoRA models with their minimum, average, and maximum performance for each training duration (in purple), and compare them to full finetuning (solid black lines) and the base model (dashed horizontal line); the results are further broken down per LoRA configuration in Fig. S2. We first note that for both domains, IFT leads to more significant improvements compared to CPT, which is expected because IFT’s problems are more similar to the evaluation problems (e.g., for code, IFT achieves maximum HumanEval of 0.50 VS 0.26 for CPT).
\ For Code CPT (Fig. 2A), we identify a substantial gap between full finetuning and LoRA that grows with more data. The overall best LoRA peaks at 16B tokens (rank=256, “All”) with HumanEval=0.175, roughly matching full finetuning with 1B tokens (HumanEval=0.172). Full finetuning reaches its peak HumanEval of 0.263 at 20B tokens. For Code IFT (Fig. 2B), the best performing LoRA (r = 256, “All”) achieves HumanEval=0.407 at epoch 4, meaningfully underperforming full finetuning at epoch 2 (HumanEval=0.464) and at its peak HumanEval score of 0.497 at 8 epochs. Math CPT (Fig. 2C) results show that training for 1B tokens or fewer degrades GSM8K results below baseline (GSM8K=0.145). Improvements appear with more data, where the best LoRA (rank=256, “All”) achieves GSM8K=0.187 at 8.6 billion tokens, underperforming full finetuning at 4.3 billion tokens (GSM8K=0.191) and at 8.6 billion tokens (GSM8K=0.230). LoRA closes
\ 
\ most of the gap with full finetuning in the Math IFT (Fig. 2D) dataset. However, LoRA still remains less sample efficient. LoRA (r = 256, “All”) peaks at 4 epochs (GSM8K=0.622) while full finetuning achieves GSM8K=0.640 at 2 epochs and peaks at 4 epochs, with GSM8K=0.642.[6] Both methods substantially exceed the base model. We hypothesize that the milder gaps here correspond to a smaller domain shift between the math problems and the pretraining data, different from the larger shifts in code.
\ In summary, across LoRA configurations and training durations, it still appears to underperform full finetuning. These effects are more pronounced for programming than math. For both domains, instruction finetuning leads to larger accuracy gains than continued pretraining.
\
:::info Authors:
(1) Dan Biderman, Columbia University and Databricks Mosaic AI (db3236@columbia.edu);
(2) Jose Gonzalez Ortiz, Databricks Mosaic AI (j.gonzalez@databricks.com);
(3) Jacob Portes, Databricks Mosaic AI (jportes@databricks.com);
(4) Mansheej Paul, Databricks Mosaic AI (mansheej.paul@databricks.com);
(5) Philip Greengard, Columbia University (pg2118@columbia.edu);
(6) Connor Jennings, Databricks Mosaic AI (connor.jennings@databricks.com);
(7) Daniel King, Databricks Mosaic AI (daniel.king@databricks.com);
(8) Sam Havens, Databricks Mosaic AI (sam.havens@databricks.com);
(9) Vitaliy Chiley, Databricks Mosaic AI (vitaliy.chiley@databricks.com);
(10) Jonathan Frankle, Databricks Mosaic AI (jfrankle@databricks.com);
(11) Cody Blakeney, Databricks Mosaic AI (cody.blakeney);
(12) John P. Cunningham, Columbia University (jpc2181@columbia.edu).
:::
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
[6] We note that the original MetaMath paper reports a maximum accuracy of 0.665 when (fully) finetuning Llama-2-7B on the MetaMathQA dataset. We attribute this to small differences in hyperparameters; they trained on 3 epochs with a batch size of 128 using the AdamW optimizer, a learning rate of 2e-5, a learning rate warmup of 3%.
Tidak ada komentar:
Posting Komentar