Table of Links
2. Context
2.1. Quantum computing as a threat to cryptography
2.2. Current approaches for quantum-safe cryptography
2.3. Blockchain and the LACChain Blockchain Network
3. The vulnerabilities of blockchain technology with the advent of quantum computing
4. A Proposal for a Quantum-Safe Blockchain Network
5. Implementation and 5.1 Generation and distribution of quantum entropy
5.2. Generation of Post-Quantum Certificates
5.3. Encapsulation of the communication between nodes using quantum-safe cryptography
5.4. Signature of transactions using post-quantum keys
5.5. On-chain verification of post-quantum signatures
6. Conclusions and next steps, Acknowledgements, and References
\
5 Implementation
The implementation of our solution is composed of the following five phases:
\
-
Generation and distribution of quantum entropy.
\
-
Generation of post-quantum certificates.
\
-
Encapsulation of the communication between nodes using quantum-safe cryptography.
\
-
Signature of transactions using post-quantum keys.
\
-
On-chain verification of post-quantum signatures.
\
5.1 Generation and distribution of quantum entropy
Randomness is the cornerstone upon which cryptographic standards are built. It is used to generate the keys and seeds used in cryptographic schemes. The challenge related to the generation of randomness is the generation of truly random data. Current techniques rely on deterministic approaches - hardware utilizing classical physics, and any available inputs that might add some level of unpredictability - which leads to the generation of pseudo-random data in the vast majority of the cases. Failure to ensure sufficient randomness in cryptographic processes can lead to real-world attacks on otherwise secure systems. This even extends to quantum random number generators which is why there is a need to develop schemes for true randomness [72].
\ Conversely, quantum generation of randomness harnesses the power of the non-deterministic nature of quantum mechanics. Generating quantum random numbers [73] can be built in many ways, as has been illustrated by the various approaches used to date, including beam splitters with detectors, vacuum fluctuations in coherent light, and squeezed coherent light mechanisms, among others [74, 75]. Despite the fact that these methods are non-deterministic, they lack the ability for an end user to guarantee that the device is working correctly. This ability in a device (sometimes known as device independence or more commonly, as certifiably quantum generation) is at the heart of the qRNG, Ironbridge, used in our solution presented in this paper.
\ IronBridge generates randomness through a quantum process evaluated as quantum certifiable which utilizes a test for the violation of a Bell Inequality [76, 77] or a higher order test of a Mermin Inequality on a NISQ machine [78]. Such a violation, along with various other security tests, are taken as mathematical proof that the output could have only come from a quantum source and is non-deterministic and thus maximally random for a physical system. For the experiments in this paper, an IBM quantum computer was used to generate the entropy
\ Given the distributed nature of a blockchain, ideally each entity running a node should have its own local source of quantum entropy: a qRNG device. However, it was not feasible to provide each node with its own qRNG for our pilot, so we used a central source of quantum entropy. As discussed throughout this paper, current cryptographic schemes used in SSL/TLS are not quantum-safe, so using them to distribute the entropy would have broken the quantum-safeness at the start.
\ We decided instead to design a protocol that allowed nodes to create a quantum safe tunnel between themselves and the entropy distribution point to ensure that this communication could be considered quantum safe. In order to do this, the entropy source creates a first key, splits it into several parts, and delivers it to the node through various TLS channels. Nodes have a time out to receive the key, recompose it, and use it to authenticate against the entropy source. This is covered in more detail in Section 5.1.2.
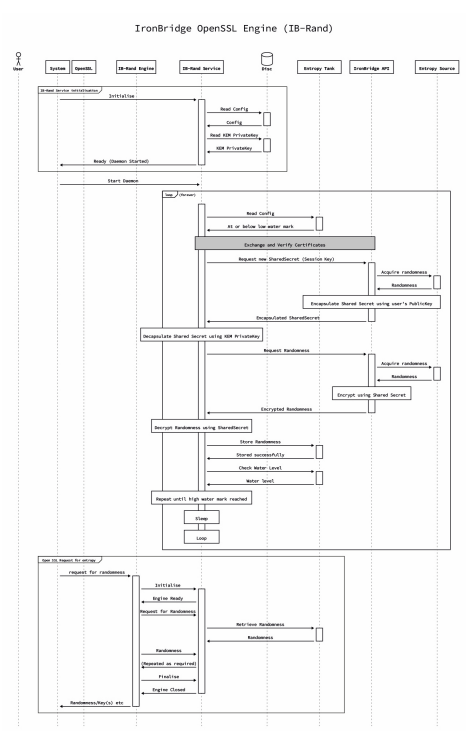
\ 5.1.1 OpenSSL Framework
\ Over the last 20 years, the OpenSSL API has become the de-facto cryptographic framework for applications that use TLS/SSL, providing capabilities such as:
\ • Generation of pseudo-random numbers.
\ • Classical cryptographic support using algorithms such as Diffie-Hellman (DH) and Elliptic Curve Diffie-Hellman (ECDH).
\ The OpenSSL applications and libraries also provide the following functions:
\ • Generation of private and public key pairs.
\ • Certificate authority management.
\ • Certificate validation.
\ • Management of crypto libraries and engine plugins to support new algorithms.
\ • SSL/TLS client and server implementations.
\ Because quantum computing will impact the security of asymmetric cryptographic algorithms such as RSA and ECDSA, the following changes within OpenSSL are required:
\ • Support for certified quantum entropy to replace the existing pseudo-random number generator used to seed keys and random values used for nonce parameters.
\ • Support for post-quantum algorithms to provide both key encapsulation and digital signatures.
\ IronBridge Platform facilitates the move to OpenSSL with entropy provided for:
\ • Quantum key encapsulation protecting existing PKI infrastructure by wrapping non-post quantum resistant keys in a post quantum wrapper.
\ • Quantum generated random numbers for pure quantum generated keys for signature digest algorithms.
\ This approach facilitates easy integration into computer security layers within the operating system while still being compatible with most of the existing infrastructure. The IronBridge Service Agent provides post quantum encapsulated key management for the secure entropy tunnel back to the IronBridge Platform. The component provides users with the ability to enforce customer security policies with regard to maximum key lifetimes by automatically providing configurable key cycling capability.
\ 5.1.2 Entropy Source Setup
\ As mentioned before, every blockchain node should ideally have its own source of quantum entropy. For our pilot, LACChain nodes did not have a local source of quantum entropy so it was necessary to establish a quantum-safe connection between the external source (the IronBridge platform) and each of the nodes. As the quantum entropy is necessary to generate the post-quantum keys that allow establishment of a quantum-safe connection, we could not use post-quantum cryptography to protect this first channel.
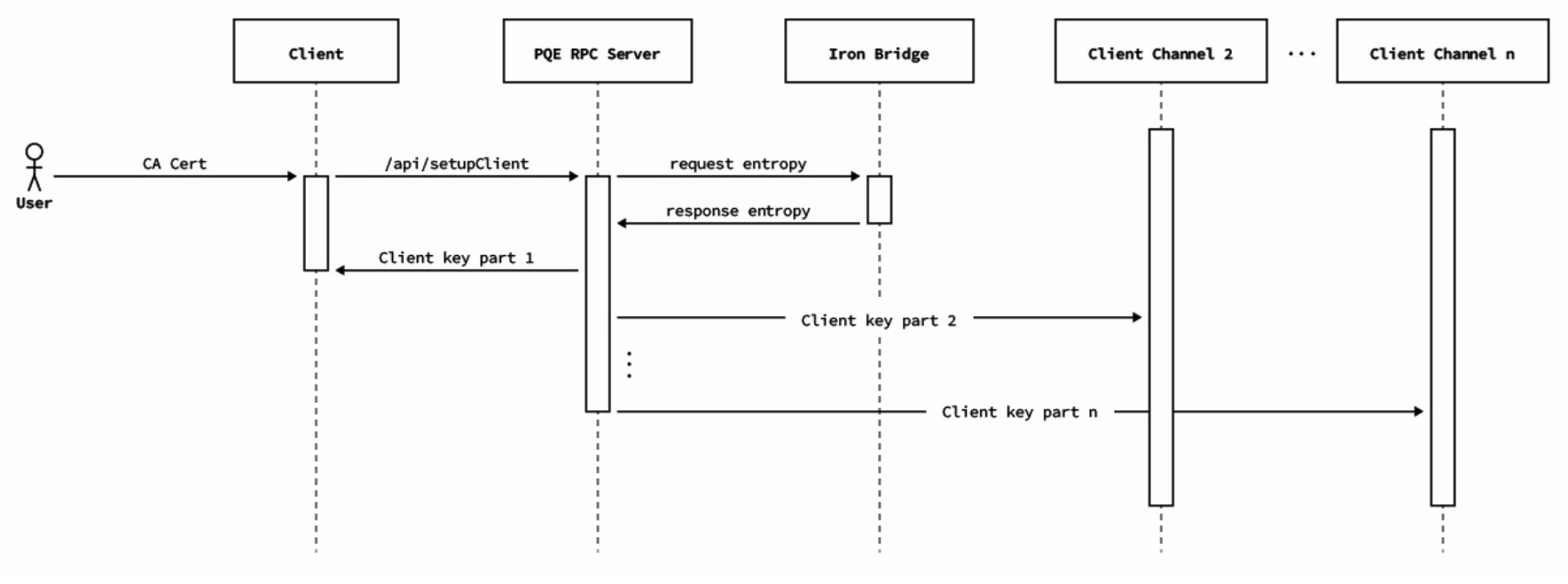
\ Therefore, we designed a protocol that begins with the distribution of a post-quantum key from the IronBridge platform to the LACChain nodes. This key is split into N parts and delivered through different TLS channels. Once the LACChain node is in possession of all the N parts, it reconstructs the key and uses it to establish a first connection with the quantum entropy source. This key is only used once, and afterwards it is immediately discarded.
\ CQC IronBridge provides certified quantum generated entropy for cryptographic use, delivering stronger classical cryptography and the highest strength post-quantum cryptography within customer’s cryptographic ecosystems. IronBridge’s patent-pending device independent certification mathematically proves every random number is the outcome of a quantum process without trusting the generation process before customer use.
\ Once this first post-quantum key is used to establish the first secure connection between the LACChain node and the entropy source, they initiate a second process to renegotiate a working KEM keypair using the post-quantum algorithm, McEliece, in line with the NIST round three submissions [41]. This allows for the establishment of a quantum-safe connection between the entropy source and the nodes which allows the LACChain nodes to start requesting quantum entropy on demand (see Fig. (1)).
\ 
\
5.2 Generation of Post-Quantum Certificates
Once the LACChain nodes have access to quantum entropy on demand, this entropy is consumed by OpenSSL as illustrated in Fig. (2). Permanent quantum-safe cryptographic solutions such as QKD (see Section 2.2.1) are not scalable today and require substantial investments in infrastructure. Feasible and practical solutions that provide quantum-resistance today involve PQC (see Section 2.2.2). Instead of replacing current Internet and blockchain protocols with new ones that incorporate PQC, we tried to introduce PQC in existing frameworks.
\ Based on the analysis presented above, we decided to use the traditional X.509 standard, which defines an internationally accepted format for digital documents that securely associates cryptographic key pairs with identities such as websites, individuals, and organizations [79].
\ By using a modified version of libSSL, the X.509 specification was extended to incorporate postquantum and Ethereum (ECDSA) public keys, allowing blockchain nodes to use the modified libSSL to establish peer-to-peer quantum-safe channels that leverage those keys. Libssl is the portion of OpenSSL that supports TLS (SSL and TLS Protocols) and depends on libcrypto.
\ As discussed in Section 4, the nodes use the post-quantum keys to encapsulate communication with other nodes and sign transactions broadcasted to the blockchain. We decided to use the same algorithm for the generation of both types of keys (i.e., encryption keys and signing keys). Given the versatility of OpenSSL to incorporate any post-quantum algorithm, the election of the post-quantum algorithm was based on the restrictions inherent in executing blockchain transactions -essentially execution time and payload size- as different algorithms present substantial differences that condition the feasibility of on-chain verifications and storage.
\ We evaluated the two finalists of the NIST competition in the signature category [41], CrystalsDilithium [49] and Falcon [50]. Figure 3 presents some of the differences between these two algorithms in terms of public key size, private key size, and signature size.
\ Both algorithms are very demanding regarding processing, memory, and amount of random material required to compute keys and signatures. However, Falcon has been acknowledged as the most compact and contains a built-in SHA3 compliant Extendable Output Function (XOF Shake256). The Ethereum VM natively supports the Keccak hashing algorithm upon which SHA 3 NIST FIPS202 is based, but it does not provide the extendable output functions (XOF) required. Further, implementing the shake XOF functionality is not straightforward.
\ We evaluated the other signing algorithms but speed, complexity, and the fact that we would have to implement a SHA3 compliant ecosystem for the qRNG source to feed those schemes proved Falcon to be the best option. Our solution allows for the incorporation of new post-quantum algorithms, such as those that can be standardized by organizations such as NIST in the upcoming months and years.
\ To use Falcon, we needed to add a new object identifier (OID), the 1.3.9999.3.1, to libSSL in order to recognize the post quantum Falcon-512 algorithm [80].
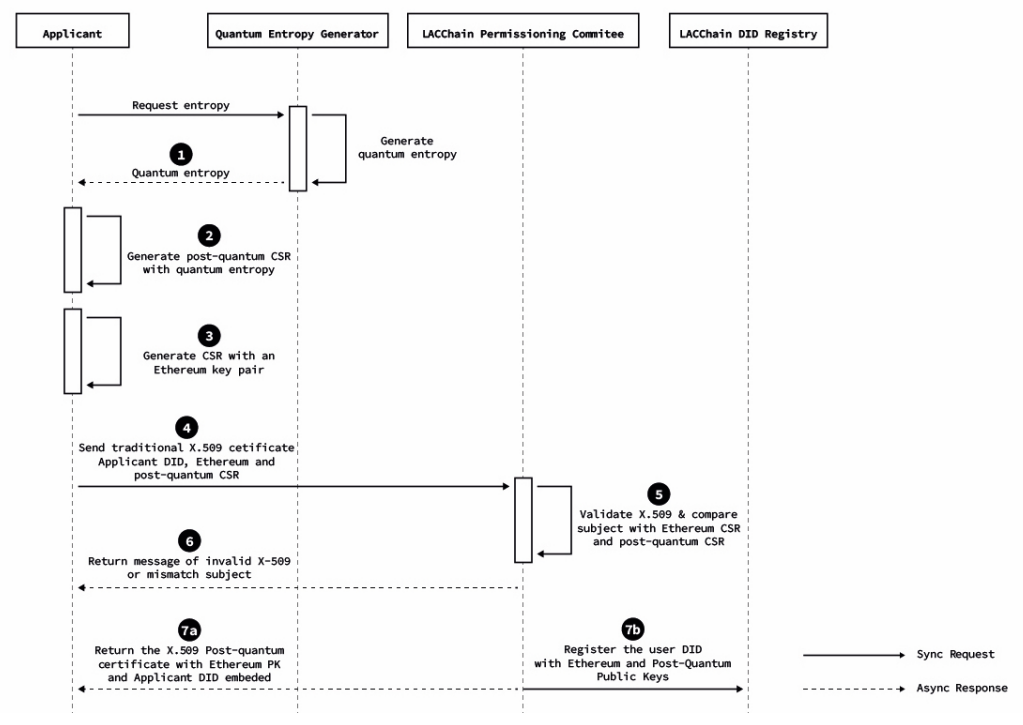
\ The process for the generation of post-quantum certificates is summarized in Figs. (4,5) and broken down into the following seven steps:
\ • The applicant requests and receives the entropy form the qRNG as explained in Section 5.1.
\ • The applicant generates a post-quantum Falcon-512 key pair using the quantum entropy through a modified version of the OpenSLL CLI (this modification has been made by the Open Quantum Safe Initiative and we have contributed with a Debian package to simplify its installation) and builds a certificate signing request (CSR).
\ \ 
\ \ \ 
\ \ • The applicant generates a second CSR with an Ethereum key pair that will be used to sign transactions using the default method set by Ethereum (currently ECDSA).
\ • The applicant sends to a certificate authority (CA) -a role played by the LACChain Technical Team in our pilot- (i) a traditional X.509 issued by a trusted CA, (ii) a certificate signing request (CSR) for the Ethereum key, and (iii) a CSR associated for the Falcon post-quantum key.
\ • The CA verifies that (i) the traditional X.509 is valid, (ii) the subject in the traditional X.509 matches the subject in the CSRs, and (iii) the signature of the CSRs matches the public keys that are requested to be certified (i.e., the CSRs are valid).
\ • If the verification fails, the certification process is rejected, and an error message is returned to the applicant.
\ • If the validation process is passed, the CA proceeds to register three items into the smart contract within the blockchain called “the Decentralized Identifier (DID) Registry.” DIDs are URIs that follow a W3C standard [81], which are suitable for the identification of individuals, entities, or other components within decentralized environments such as blockchain networks. The three items registered in the smart contract are (i) the DID, (ii) the Ethereum and Falcon post-quantum public keys, and (iii) the subject data or alternatively a proof of the subject’s identity that does not reveal subject data. Simultaneously, the CA also returns several items to the applicant, including the Falcon post-quantum X.509 certificate that contains the Ethereum public key, the Falcon post-quantum public key, and a new DID controlled by another DID derived from the ETH key.
\ Each of these steps is essential and additional useful clarifications are listed below:
\ • CSR are files of encoded text that contain information to be included in the requested certificate such as the organization name, common name (domain name), address, and country. It also contains the public key that will be included in the certificate, but the private key is not disclosed. Instead, the private key is used to sign the request so the CA can verify that the requester is indeed in control of that particular private key.
\ • The applicant is required to present a traditional X.509 so the blockchain CA does not have to accomplish the verification of the applicant’s identity from scratch. Both the applicant and the CA take advantage of a previous X.509 and the CA only verifies that the certified subject data in the X.509 matches the subject data in the CSRs.
\ \ 
\ \ • The DID Registry follows the DID standard from the W3C [81] which presents a data model for identifiers particularly designed to be resolved and verified in decentralized registries. Every time the CA certifies a new entity, it registers the DID in the blockchain with the information about the certified Ethereum and Falcon public keys, so that anyone with access to the public blockchain ledger can resolve the entity’s DID and verify the keys associated with them. For example, this would occur when the entity is using the Ethereum key, the Falcon key, or both to sign a transaction, which will be addressed in Subsection 5.5.
\
:::info Authors:
(1) M. Allende, IDB - Inter-American Development Bank, 1300 New York Ave, Washington DC, USA and LACChain - Global Alliance for the Development of the Blockchain Ecosystem in LAC;
(2) D. López Leon, IDB - Inter-American Development Bank, 1300 New York Ave, Washington DC, USA and LACChain - Global Alliance for the Development of the Blockchain Ecosystem in LAC;
(3) S. Ceron, IDB - Inter-American Development Bank, 1300 New York Ave, Washington DC, USA and LACChain - Global Alliance for the Development of the Blockchain Ecosystem in LAC;
(4) A. Leal, IDB - Inter-American Development Bank, 1300 New York Ave, Washington DC, USA and LACChain - Global Alliance for the Development of the Blockchain Ecosystem in LAC;
(5) A. Pareja, IDB - Inter-American Development Bank, 1300 New York Ave, Washington DC, USA and LACChain - Global Alliance for the Development of the Blockchain Ecosystem in LAC;
(6) M. Da Silva, IDB - Inter-American Development Bank, 1300 New York Ave, Washington DC, USA and LACChain - Global Alliance for the Development of the Blockchain Ecosystem in LAC;
(7) A. Pardo, IDB - Inter-American Development Bank, 1300 New York Ave, Washington DC, USA and LACChain - Global Alliance for the Development of the Blockchain Ecosystem in LAC;
(8) D. Jones, Cambridge Quantum Computing - Cambridge, United Kingdom;
(9) D.J. Worrall, Cambridge Quantum Computing - Cambridge, United Kingdom;
(10) B. Merriman, Cambridge Quantum Computing - Cambridge, United Kingdom;
(11) J. Gilmore, Cambridge Quantum Computing - Cambridge, United Kingdom;
(12) N. Kitchener, Cambridge Quantum Computing - Cambridge, United Kingdom;
(13) S.E. Venegas-Andraca, Tecnologico de Monterrey, Escuela de Ingenieria y Ciencias. Monterrey, NL Mexico.
:::
:::info This paper is available on arxiv under CC BY-NC-ND 4.0 DEED license.
:::
\
Tidak ada komentar:
Posting Komentar